Last updated on
K-Window Minimum
- Points
- 100 pts
- Topics
- Data Structures, Trees, Recursion, Debugging
- Files to Submit
src/main/scala/kwindow/KWindow.scalasrc/main/scala/kwindow/AVLOrderedSet.scala
Introduction
In this mini-lab, we will illustrate the famous equation “Programs = Algorithms + Data Structures”.
The $k$-window Minimum problem asks, for a sequence of items xs of size at least $k$,
compute a sequence, ms, where each element is the minimum value
of the corresponding $k$-window of the original sequence.
For example, for the following sequence of integers: $$ 1, 4, 6, 2, 5 $$ and $k = 3$, the corresponding $k$-window minimum sequence is $1, 2, 2$.
Step by Step
We can consider each $3$-window of the sequence and find the minimum as the following table demonstrates:
| Sequence | Window | Minimum |
|---|---|---|
| 1, 4, 6, 2, 5 | 1, 4, 6 | 1 |
| 1, 4, 6, 2, 5 | 4, 6, 2 | 2 |
| 1, 4, 6, 2, 5 | 6, 2, 5 | 2 |
Is it just too simple?
Of course, in Scala, a simple solution to this problem is to find the minimum over a sliding window:
def kWindowMinSimple[A](xs: Seq[A], k: Int)(using ord: Ordering[A]): Seq[A] =
require(k > 0)
require(xs.size >= k)
xs.sliding(k).map(_.min).toSeq
kwindow/./src/test/scala/KWindow.scala
However, this is very inefficient! We are re-calculating the minimum of every window, so our simple solution cannot handle longer sequences.
In this task, we will implement a more efficient solution to this problem with the help of an Ordered Set data structure.
What are Ordered Sets?
Ordered Sets are an extension of Multi-Sets, supporting the following operations:
- Insert a new value into the set.
- Remove a value from the set.
- Check whether the set contains a value.
- Get the minimum value of all values in the set.
Note that unlike Scala Set, ordered sets can have multiple copies of the same value,
and the remove operation removes only one instance of the value (if it exists).
In Scala, we define the OrderedSet interface as a trait with the above
operations as follows:
/** An ordered set of items of type `A`. Supports querying, insertion, deletion
* of items as well as getting the minimum item.
*/
trait OrderedSet[A]:
/** Returns the size of the tree. */
def size: Int
def isEmpty: Boolean = size == 0
/** Returns a new [[OrderedSet]] with one instance of `item` inserted. */
def insert(item: A): OrderedSet[A]
/** Returns a new [[OrderedSet]] with one instance of `item` removed. */
def remove(item: A): OrderedSet[A]
/** Returns whether `item` is contained in the set. */
def contains(item: A): Boolean
/** Returns the minimum item contained in the tree.
* @throws NoSuchElementException
* if the tree is empty.
*/
def getMin: A
kwindow/./src/main/scala/kwindow/OrderedSet.scala
Other than the four main operations (insert, remove, contains and getMin),
the Scala ordered set also supports getting the size and query whether the
set isEmpty.
Implementing K-Window using Ordered Sets
Now that we know what an ordered set is, let’s try to solve $k$-window minimum with using ordered sets!
💪 Task: Implement kWindowMin (50 pts)
Implement kWindowMin. Your function should have the following signature:
/** Given a window size `k` > 0 and a sequence of items `xs` (of length at least
* `k`), return a sequence that is a k-window minimum sequence of `xs`.
*/
def kWindowMin[A](
xs: Seq[A],
k: Int,
emptySet: OrderedSet[A]
): Seq[A] =
require(k > 0)
require(xs.length >= k)
???
kwindow/./src/main/scala/kwindow/KWindow.scala
You are free to chose your algorithm, but it must use the provided emptySet, and its complexity must be no more than $\mathcal{O}(n \times c)$, where $n$ is the number of elements in xs and $c$ is the cost of removing or adding an element to the ordered set. We suggest the following algorithm:
- Construct an initial ordered set
sfrom the firstkelements ofxs. - For each remaining element
eof the sequence, remove the oldest element ofsand addeto the ordered set. - At each step, extract the minimum of the set.
Note that you are given, in addition to the sequence xs and k, an empty
OrderedSet[A].
You can run tests for this task using the testOnly command.
sbt:kwindow> testOnly -- *kWindowMin:*
Note that the tests are run with a NaiveOrderedSet implementation,
which is not yet using an efficient ordered set, which we will work with in the next task!
We shall move to the more efficient AVLOrderedSet implementation in the next section, when
we are sure our kWindowMin implementation is tested.
AVL Trees
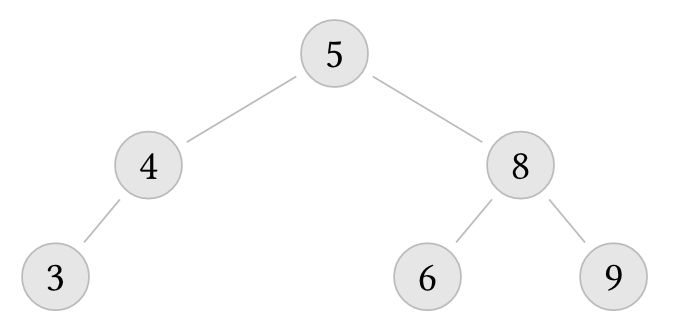
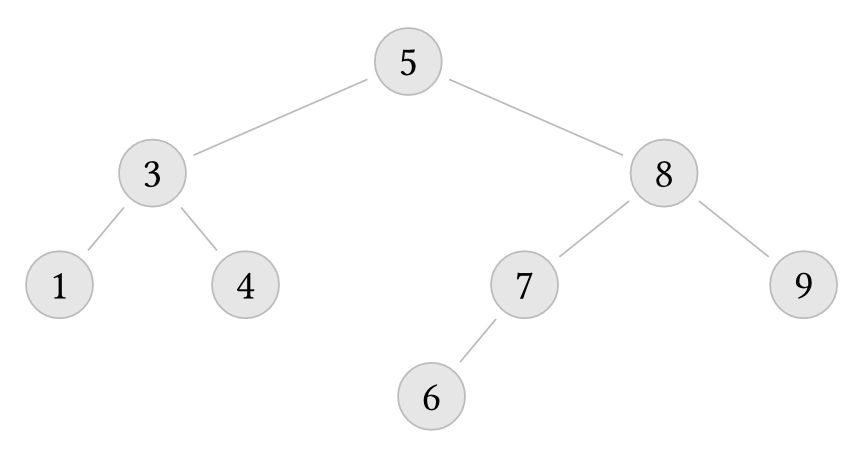
Ordered Sets are usually implemented as binary search trees, where the item at the root of the tree is larger than or equal to all of the items in its left subtree, and smaller than or equal to all of the items in its right subtree. We call this condition the binary search tree (BST) condition of the tree.
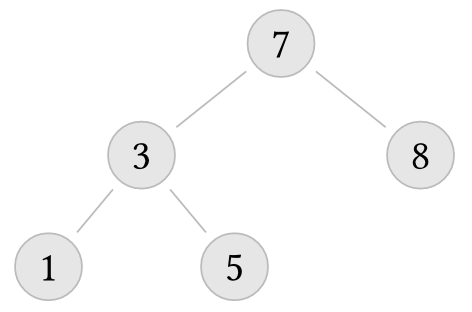
Examples of BSTs
The following trees satisfy the BST condition:
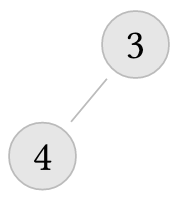
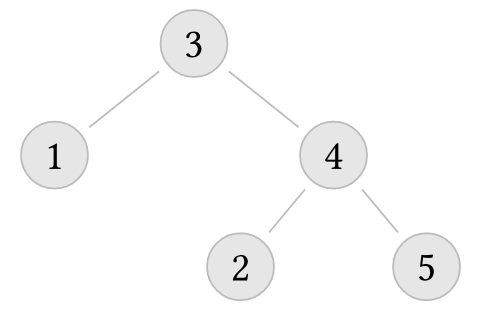
But the following trees do not
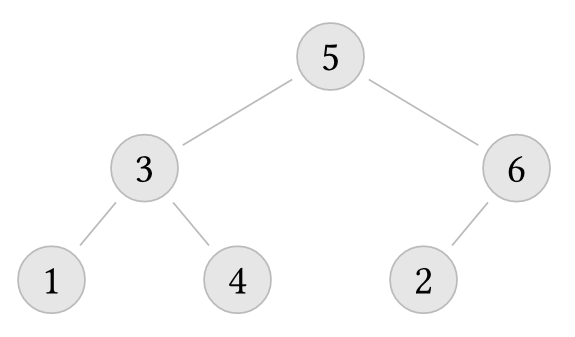
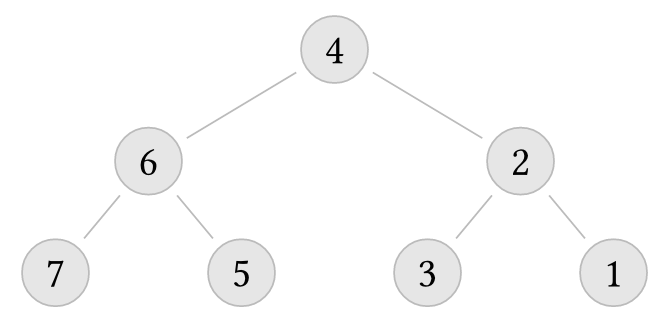
Note that a child sub-tree that is empty is simply omitted from the diagram.
On a binary search tree, obtaining the minimum value is simple: it is on the leftmost node of the tree!
We will be looking at a particular kind of BST implementation called AVL Trees.
Valid AVL Trees are binary search trees satisfying the following requirements:
- An empty tree is a valid AVL tree (of height 0).
- A non-empty tree is a valid AVL tree if:
- Both its children are valid AVL trees, and
- The difference between the height of the left subtree and the right subtree is at most 1.
The height of a tree is defined to be the longest path (in number of nodes) from the root to an empty node.
For simplicity, we sometimes omit the “valid” part and say just “AVL tree”.
Examples
The following trees are valid AVL trees (i.e., they verify the properties above):




But the following trees are not AVL trees:

In Scala, a Tree is defined as either Empty, or a Node with
one value and two sub-Trees:
/** A binary tree containing items of type `A`. */
enum Tree[+A]:
case Empty
case Node(item: A, left: Tree[A], right: Tree[A])
/** The height of the tree. */
lazy val height: Int = this match
case Empty => 0
case Node(item, left, right) => left.height.max(right.height) + 1
kwindow/./src/main/scala/kwindow/AVLOrderedSet.scala
An AVLOrderedSet, being a binary search tree, also needs to know how the ordering of the
elements are defined:
/** AVL tree is a balanced Binary Search Tree, implementing the [[OrderedSet]]
* trait.
*
* It contains a [[Tree]] of items, sorted by the given
* [[scala.math.Ordering]].
*/
case class AVLOrderedSet[A] private (tree: Tree[A])(using
private val ord: Ordering[A]
) extends OrderedSet[A]:
// ...
kwindow/./src/main/scala/kwindow/AVLOrderedSet.scala
… where Ordering[A] defines the ordering of A through its
compare, lt (less than) and gt (greater than) methods.
💪 Task: Is a Tree a valid AVL Tree? (20 pts)
Implement the function isValidAVLTree, that takes a Tree and an Ordering, and
returns whether the tree satisfies the requirements
of an AVL tree.
/** Returns whether the given [[Tree]] is a valid AVL tree with respect to the
* given [[Ordering]].
*/
def isValidAVLTree[A](tree: Tree[A])(using ord: Ordering[A]): Boolean =
???
kwindow/./src/main/scala/kwindow/AVLOrderedSet.scala
You can run tests for this task using the testOnly command.
sbt:kwindow> testOnly -- *isValidAVLTree*
Using kWindowMin with AVL Trees
With our kWindowMin implementation ready and tested, let’s try to combine it with an efficient
ordered set implementation, so that our solution can fully handle tens of thousands of elements.
💪 Task: Fix the AVL Tree! (30 pts)
This is the final task of this exercise. You should only continue when you have passed all testcases from the last tasks!
We asked an anonymous CS-214 TA to provide you with an implementation of Ordered Set operations
for AVL trees, that you can freely use.
However, due to lack of sleep and overusage of coffee, the implementation is rushed and
not well tested, so there might be a bug in one of the methods in the AVLOrderedSet class!
The TA promises however that you only have to change at most one line of code to get it working…
Your task is to debug the AVL tree implementation so that kWindowMin
tests using AVLOrderedSets pass.
You can run tests for this task using the testOnly command.
sbt:kwindow> testOnly -- "*kWindowMin with AVLOrderedSet: *"
You should find details on the implementation of AVL Tree in the docstrings
within AVLOrderedSet.scala.