Last updated on

Lab 5: Anagrams

What do the words Suisse and Issues have in common? They are anagrams of each other! Two words are called anagrams if they have the same letters, albeit in a different order. Sentences can also be anagrams of each other:

Finding anagrams is a tricky combinatorial problem: the letters in a sentence like I AM LORD VOLDEMORT, with 19 characters, can be reordered in $19!$ ways, which is…

scala> def fact(n: BigInt): BigInt =
     |   if n == 1 then 1 else n * fact(n-1)
     | fact(19)
def fact(n: BigInt): BigInt
val res0: BigInt = 121645100408832000

… a lot. In this lab, we’ll create an anagram solver: a program capable of searching through a large space of potential anagrams more efficiently than by brute-force enumeration.

This lab aims to exercise the following concepts and techniques:

  • Types and type aliases
  • Structural recursion
  • Collections and their APIs
  • Comprehensions and combinatorial search

Logistics

📝 Important: Don’t forget to fill in how many hours you spent on this lab in howManyHoursISpentOnThisLab() in src/main/scala/HowManyHoursISpentOnThisLab.scala to pass the final test!

How to make the most of this lab

The point of this lab is to train you to use collections and their APIs: we have designed the assignment so that almost all of it can be solved by combining built-in functions and for comprehensions. Hence, if you find yourself writing a complicated recursive function, think again!

Useful documentation for Scala collections can be found here:

Problem statement

An anagram of a word is another word that can be formed by rearranging the letters of the first. For example, integral is an anagram of triangle, and logarithm is an anagram of algorithm.

In a similar way, an anagram of a sentence is a different sentence that can be formed by rearranging all the letters of the first. The new sentence must consist of meaningful words, but the number of words, punctuation, case, or even accents do not have to match. For example, You olive is an anagram of I love you. Plain permutations, such as you I love, are also anagrams for our purposes.

Your ultimate goal is to implement a method anagrams, which, given a collections of letters and a list of permissible words, finds all anagrams of that sentence composed of valid words.

Take a moment to think about this problem. If you have not completed it yet, also consider taking a moment to solve the 🧪 exercises in this week’s exercise set, especially the Des lettres part of Des chiffres et des lettres.

The approach in the first part of this lab is relatively inefficient; to keep your workload reasonable, we’ve left optimizations to callbacks.

Approach

To find sentence anagrams, we will break our sentence into individual letters, enumerate all subsets of these letters, check each subset to see if it is an anagram of a known word, and if so recursively combine it with sentence anagrams of the rest of the sentence.

For example, the sentence You olive has the letters eiloouvy:

  1. Start by identifying a subset, say elov. We are left with the characters iouy.
  2. Consult the word list to see that elov is an anagram of love.
  3. Solve the problem recursively for the rest of the characters (iouy), obtaining List(I, you), and List(you, I).
  4. Combine the word love to obtain six possible results:
    • List(love, I, you),
    • List(love, you, I),
    • List(I, love, you),
    • List(you, love, I),
    • List(I, you, love), and
    • List(you, I, love).

This process requires:

  1. Normalizing all inputs to remove diacritics (accents) and non-alphabetic characters (punctuation, spaces, etc.)
  2. Constructing a dictionary to quickly look up word anagrams
  3. Recursively enumerating subsets of a given set
  4. Recursively constructing sentence anagrams

… which is what we’ll do!

Efficient Tree Representation

Grouping Common Prefixs

As we have seen above, a naive implementation would use lists of sentences to represent anagrams, for example anagrams of the sentence “no mercy” can be represented as:

List("cry", "me", "no")
List("cry", "me", "on")
List("cry", "no", "me")
List("cry", "on", "me")

List("me", "no", "cry")
List("me", "on", "cry")
List("me", "cry", "no")
List("me", "cry", "on")

List("no", "cry", "me")
List("no", "me", "cry")

List("on", "cry", "me")
List("on", "me", "cry")

However, prefixes are duplicated in the lists. Is it necessary? For example, can we group sentences starting with “cry” together with a single copy of “cry”?

Back in the find lab, we can easily reason about the list of output files as a tree. For example,

food/
food/fruits/
food/fruits/strawberry.txt
food/fruits/tomato.txt
food/vegetables/
food/vegetables/tomato.txt

is naturally equivalent to the following tree:

food
├── fruits
│   └── strawberry.txt
│   └── tomato.txt
└── vegetables
    └── tomato.txt

because the list and tree representation share the same prefix paths.

Applying this reasoning to anagrams, we notice that trees are a very natural structure to represent anagrams of a sentence. The following tree represents the previous anagram lists of “no mercy”:

.
├── cry
│   ├── me
│   │   ├── no
│   │   └── on
│   ├── no
│   │   └── me
│   └── on
│       └── me
├── me
│   ├── cry
│   │   ├── no
│   │   └── on
│   ├── no
│   │   └── cry
│   └── on
│       └── cry
├── no
│   ├── cry
│   │   └── me
│   └── me
│       └── cry
└── on
    ├── cry
    │   └── me
    └── me
        └── cry

As you can notice, grouping parts of sentences by prefix gives a more concise representation.

Grouping Equivalent Words

We can go further: both “no” and “on” are composed of the same letters, which means that in the context of anagrams they are equivalent.

Formally, they are part of the same equivalence class. An equivalence class is a set where any two elements are equivalent under a equivalence relation. Here, our equivalence class is a set of words (type EquivalenceClass = Set[Word]), and the equivalence relation is being anagrams with each other. An equivalence relation $\sim$ on a set $X$ should satisfy three properties:

Could you convince yourself that the anagram relation indeed satisfies these properties?

If we group the equivalent words together in a single set, we can shorten the representation of our sentence even more:

.
├── cry
│   ├── me
│   │   └── {no, on}
│   └── {no, on}
│       └── me
├── me
│   ├── cry
│   │   └── {no, on}
│   └── {no, on}
│       └── cry
└── {no, on}
    ├── cry
    │   └── me
    └── me
        └── cry

In a graphical visualisation:

treeReduce
Tree representation of the anagrams of the sentence "no mercy"

We could go even further by grouping sentences that are composed of the same words but in a different order in a single branch. In our example, this would result in a single branch tree, accounting for all sentences above:

.
└── cry
    └── me
        └── {no, on}

However this optimisation is left as an optional callback on this lab.

Implementation guide

If you want to follow the Senior track of this lab, start implementing your own custom solution without reading this section. Skip to the Senior track section for instructions.

We represent words of a sentence with the String data type, and sentences as lists of Words:

type Word = String
type Sentence = List[Word]

src/main/scala/anagrams/Anagrams.scala

The tree type is already defined for you insrc/main/scala/cs214/AnagramsTree.scala:

/** An `AnagramsTree` is a compact tree representation of a collection of
  * anagrams
  */
type AnagramsTree = List[Branch]

src/main/scala/cs214/AnagramsTree.scala

/** A branch represents a (subpart) of a sentence of anagrams */
case class Branch(val headWords: EquivalenceClass, val suffixes: this.AnagramsTree)

Can you construct the following tree in code ?

treeReduce
Simple tree example
Solution 
val tree: AnagramsTree = List(
  Branch(Set("a"), Nil),
  Branch(Set("bc", "cb"), List(
    Branch(Set("de", "ed"), Nil),
    Branch(Set("f"), Nil)))
)

The code representation of trees is not very readable for us humans, that’s why we would like to better visualize it in some way. The AnagramsTree.show function takes care of that. It follows the format of the tree UNIX command. The above tree would be displayed as follows:

.
├── a
└── {bc, cb}
    ├── {de, ed}
    └── f

Encoding issues may cause your terminal to print unexpected symbols (“Mojibake”) when instead of the nice tree displayed above when you test your program. If so, follow the instructions from this Ed post (or return to the train example in the debugging lecture!) to fix the problem.

Canonicalization

To find anagrams of a single word, we could simply go through the whole word list and check for each entry whether it is an anagram of our input word. Unfortunately, this is not very efficient: we would need to scan the whole word list every time.

Instead, we will use a simple and very useful trick called canonicalization. Canonicalization is the process by which we translate multiple equivalent inputs (such as the words “eat” and “tea”) to a unique canonical representation, which we can then use to check equivalence quickly.

In Des lettres, we canonicalized words by “scrambling” them: converting them to uppercase and sorting them. scramble was such that two words $w_1$ and $w_2$ were anagrams if and only if scramble($w_1$) == scramble($w_2$):

scala> println(scramble("eat"))
AET
scala> println(scramble("tea"))
AET

Multisets

The key observation here is that two words are anagrams of each other if the multisets of their letters are equal. To make use of this observation in practice, we’ll need to implement multisets. More specifically, we’ll have to:

  1. Chose a type to represent a multiset containing elements of type T;
  2. Implement relevant operations (subsets and subtract);
  3. Implement a function to convert a list into a multiset (from).

To give you more freedom, we have left the type of multisets unspecified. That is, you are free to chose which data structure you’d like to use! It could be trees, or sorted lists, or any other structure of your choice, but beware: it must be canonical (that is, the representation of a given multiset should be unique). We provide a suggestion below, if you prefer a more guided experience.

A suggested implementation: occurrence lists

Occurrence lists represent a multiset as a sorted list of distinct elements, each paired with their multiplicity (the number of times each element appears in the multiset). For example, the multiset {a, a, a, b, c, c} is represented as List(('a', 3), ('b', 1), ('c', 2)).

Concretely, we suggest using the following type:

type MultiSet[+A] = List[(A, Int)]

Each entry in the list denotes an element and how many times it occurs. The integer must be positive: elements that do not appear in the multiset must not appear in the list either.

Your task is to complete the following functions in src/main/scala/anagrams/MultiSet.scala according to their documentation:

Use the List and Map APIs and for comprehensions! The functions groupBy, map, and sorted may come in handy.

subsets
/** Returns the list of all subsets of a given MultiSet
  *
  * This always includes the original multiset itself and the empty multiset.
  *
  * For example, the subsets of `{a, a, b}` are `{}, {a}, {a, a}, {b}, {a, b},
  * {a, a, b}`
  *
  * Note that the order in which subsets are returned does not matter.
  * However, individual subsets must remain canonical.
  */
def subsets: List[MultiSet[A]] =
  ???

src/main/scala/anagrams/MultiSet.scala

How is {a, a, b} represented as an occurrence list? How are its subsets represented? Can you leverage the structure of occurrence lists to compute subsets efficiently?

Solution

The corresponding occurrence list is List(('a', 2), ('b', 1)). There are 6 subsets:

List(),
List(('a', 1)),
List(('a', 2)),
List(('b', 1)),
List(('a', 1), ('b', 1)),
List(('a', 2), ('b', 1)))
Constructing subsets efficiently

To solve this question, ask yourself: what equations does the subsets function obey? In other words, if you have the subsets of a multiset $m$, how can you construct the subsets of a multiset $M$ that has all the pairs in $m$ plus an additional element $x$ with multiplicity $k$ (that is, M = (x, k) :: m)?

subtract
/** Subtracts multiset `other` from this multiset
  *
  * For example, `{1,2,2,2,3,4,4} - {1,1,2}` is `{2,2,3,4,4}`.
  *
  * Note: the resulting set must be a valid multiset: it must be canonical and
  * have no zero entries.
  */
def subtract(other: MultiSet[A]): MultiSet[A] =
  ???

src/main/scala/anagrams/MultiSet.scala

Here too, think of how this function operates on multisets. How does the example given in the documentation above translate in terms of occurrence lists?

Solution 
val big = List((1,1), (2,3), (3,1), (4,2))
val small = List((1,2), (2,1))
big.subtract(small) // List((2,2), (3,1), (4,2))

Remember that MultiSet[+A] is a generic type, so your solution can’t re-sort the result: you must preserve the ordering as you compute the subtraction!

from
/** Creates a MultiSet from a given sequence, using the given comparison
  * function.
  *
  * @param lt
  *   the comparison function which tests whether its first argument precedes
  *   its second argument in the desired ordering.
  * @see
  *   https://dotty.epfl.ch/api/scala/collection/SeqOps.html#sortWith
  */
def from[A](seq: Seq[A])(lt: (A, A) => Boolean): MultiSet[A] =
  ???

src/main/scala/anagrams/MultiSet.scala

If using occurrence lists, what should MultiSet.from(List(3,1,2,4,2,2,4))(_ < _) return?

Solution

List((1,1), (2,3), (3,1), (4,2)).

Bags of letters

Going back to anagrams, each word can be now transformed into a unique multiset. For succinctness, we call these multisets of characters LetterBags:

/** A `LetterBag` is a multiset of lowercase letters. */
type LetterBag = MultiSet[Char]

src/main/scala/anagrams/Anagrams.scala

How are the letter bags corresponding to the words "tea" and "better" represented?

Solution

If you used occurrence lists, you would get the following letter bags:

  • "tea": List((a, 1), (e, 1), (t, 1))
  • "better": List((b, 1), (e, 2), (r, 1), (t, 2))

Constructing such a letter bag is straightforward: we first remove all diacritics (accents) and non-alphabetic characters (punctuation, spaces, etc.), and then construct a multiset:

/** Normalizes a string `str` and converts it into a LetterBag. */
def computeLetterBag(str: String): LetterBag =
  MultiSet.from(normalizeString(str))(_ < _)

src/main/scala/anagrams/Anagrams.scala

Computing anagrams of a word

To compute the anagrams of a word, we use the simple observation that all the anagrams of a word have the same letter bag. To allow efficient lookup of all the words with the same letter bag, we will have to group the words of the word list according to their occurrence lists.

For this purpose, we define the type Dictionary:

/** A `Dictionary` is a mapping from letter bags to corresponding words.
  *
  * For example, if the original word list contains the entries `ate`, `eat`,
  * `tea`, `ball`, then the resulting `Dictionary` will contain two entries:
  * {{{
  * {a, e, t} -> Set("ate", "eat", "tea")
  * {a, b, l, l} -> Set("ball")
  * }}}
  */
type Dictionary = Map[LetterBag, EquivalenceClass]

src/main/scala/anagrams/Anagrams.scala

In src/main/scala/anagrams/Anagrams.scala, implement the function createDictionary:

/** Constructs a dictionary from a word list. The keys of the resulting map are
  * letter bags. The values are sets of words that share the same letters. This
  * map makes it easy to obtain all the anagrams of a word given its letters.
  */
def createDictionary(wordlist: Set[String]): Dictionary =
  ???

src/main/scala/anagrams/Anagrams.scala

Sentence anagrams

Anagrams of a sentence

With this, you have all pieces in hand to implement the function anagrams. This function takes two arguments:

  1. a dictionary, created from a wordlist using createDictionary above;
  2. a bag of letters (e.g. {a, a, a, b, n, n}) of type LetterBag, from which you should create anagrams.

Here is how you might call this function:

import cs214.{loadWordlist, show}

object NGSL:
  val wordlist = loadWordlist("en-ngsl")
  val dictionary = createDictionary(wordlist)

val letters = MultiSet.from("banana")(_ < _)
anagrams(NGSL.dictionary, letters).show

src/main/scala/playground.worksheet.sc

Your task is to construct a tree of complete anagram sentences composed of words taken from the dictionary. The documentation of the function is shown below:

/** Returns a tree of all complete anagram sentences of the given letters using
  * words from the given dictionary.
  *
  * @param dict
  *   A dictionary of known words, grouped into equivalence classes.
  * @param letters
  *   The letters to create an anagram from.
  *
  * For example, when given {a, a, a, b, n, n} (the letters in “banana”) anagram
  * could produce the following tree:
  * {{{
  * .
  * ├── a
  * │   ├── an
  * │   │   └── ban
  * │   └── ban
  * │       └── an
  * ├── an
  * │   ├── a
  * │   │   └── ban
  * │   └── ban
  * │       └── a
  * ├── ban
  * │   ├── a
  * │   │   └── an
  * │   └── an
  * │       └── a
  * └── banana
  * }}}
  * Which corresponds to this Scala entity:
  * {{{
  * List(
  *   Branch(Set("a"),List(
  *     Branch(Set("an"),List(
  *       Branch(Set("ban"),Nil))),
  *     Branch(Set("ban"),List(
  *       Branch(Set("an"),Nil))))),
  *
  *   Branch(Set("an"),List(
  *     Branch(Set("a"),List(
  *       Branch(Set("ban"),Nil))),
  *     Branch(Set("ban"),List(
  *       Branch(Set("a"),Nil))))),
  *
  *   Branch(Set("ban"),List(
  *     Branch(Set("a"),List(
  *       Branch(Set("an"),Nil))),
  *     Branch(Set("an"),List(
  *       Branch(Set("a"),Nil))))),
  *
  *   Branch(Set("banana"), Nil),
  * )
  * }}}
  *
  * The different sentences do not have to be output in the order shown above:
  * any order is fine as long as all the anagrams are there. Every word returned
  * has to exist in the dictionary.
  *
  * Note: If the words of the sentence are in the dictionary, then the sentence
  * is an anagram of itself, and it must appear in the result.
  */
def anagrams(dict: Dictionary, letters: LetterBag): AnagramsTree =
  ???

src/main/scala/anagrams/Anagrams.scala

Start by thinking on paper, and do not code until you have a clear idea of what the algorithm should do. The final implementation is just 5 lines long.

Using for comprehensions helps in formulate the solution of this problem elegantly.

Remember that valid anagrams should use all letters of the input! “quietly hot” is not an anagram of “poly technique”, because the letters e, n, and p are missing.

Test the anagrams method on short sentences (no more than 10 characters). The combinations space gets huge very quickly as your sentence gets longer, so the program may run for a very long time if you give it long sentences.

Senior track

To follow the senior track of this lab, you should not take a look at the Implementation guide section. Instead, come up with your own MultiSet[+A] implementation, along with the three suggested functions:

extension [A](set: MultiSet[A])
  def subsets: List[MultiSet[A]]
  def subtract(other: MultiSet[A]): MultiSet[A]

object MultiSet:
  def from[A](seq: Seq[A])(lt: (A, A) => Boolean): MultiSet[A]

Usage

To help you enjoy your cool new program, we’ve implemented a command line interface. You can call it from the sbt terminal using the run command. Its syntax is as follows:

sbt> run [--wordlist <name>] <word> [<word>…]

Compute sentence anagrams of a collection of words.

Options:

  • --wordlist <path>: load an alternate wordlist. Available wordlist are en-ngsl, fr-edu, en-debian, en-able, and fr-lp.

Warning : The algorithm does not restrict the size of the sentence you put as an argument. Processing a long sentence will take a lot of time.

We have included the following wordlists:

Here are some examples:

sbt> run teacher
.
├── he
│   └── {react, trace}
├── {care, race}
│   └── the
├── here
│   └── {act, cat}
├── {act, cat}
│   └── here
├── the
│   └── {care, race}
├── {react, trace}
│   └── he
└── teacher

sbt> run professeur --wordlist fr-edu
.
├── fer
│   ├── près
│   │   └── sou
│   ├── sou
│   │   └── près
│   └── pousser
├── près
│   ├── fer
│   │   └── sou
│   └── sou
│       └── fer
├── presser
│   └── fou
├── fou
│   └── presser
├── sou
│   ├── fer
│   │   └── près
│   └── près
│       └── fer
├── pousser
│   └── fer
└── professeur

Optional challenge: Lausannagrams! (optional)

A few years ago, a humorous map of the Boston metro was making the rounds. This is the original metro map (source: Wikipedia):

And this is the anagramed version (source):

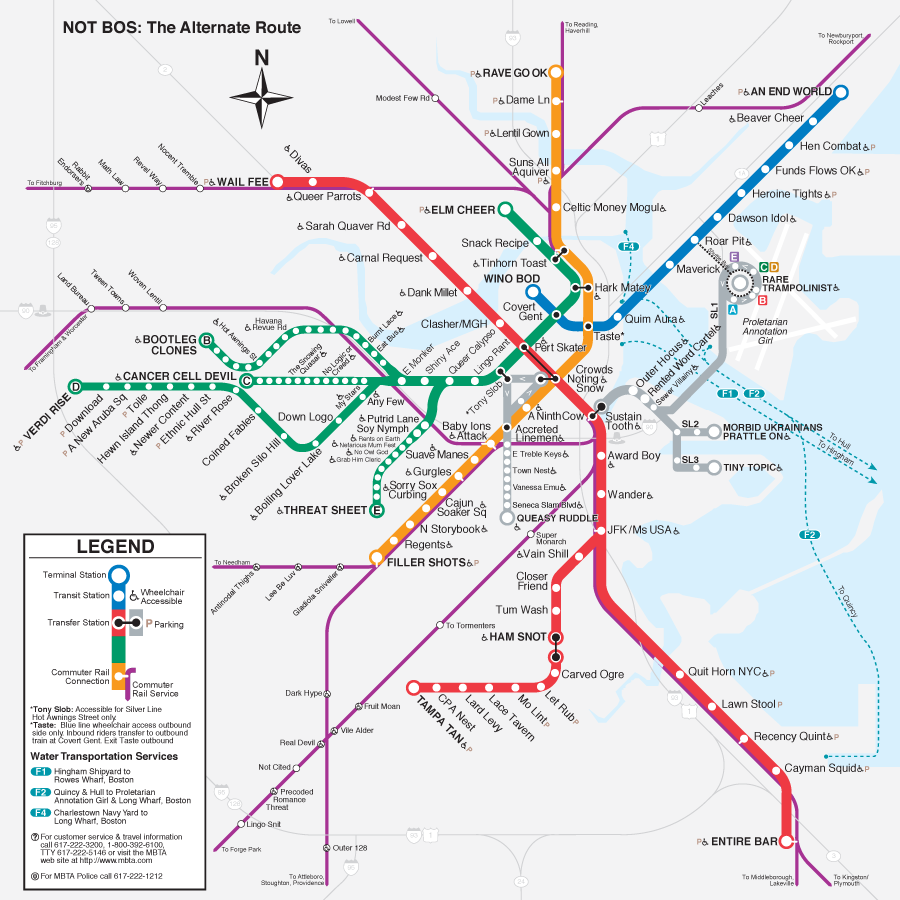
We were not able to find a similar map for Lausanne, or Vaud. Can you help? You can use this map to find inspiration.

Share your suggestions on Ed! We have the following:

© 2023, 2024 EPFL. All rights reserved.